Brechung/Dioptrien und Sehschärfe/Visus
Diagramm
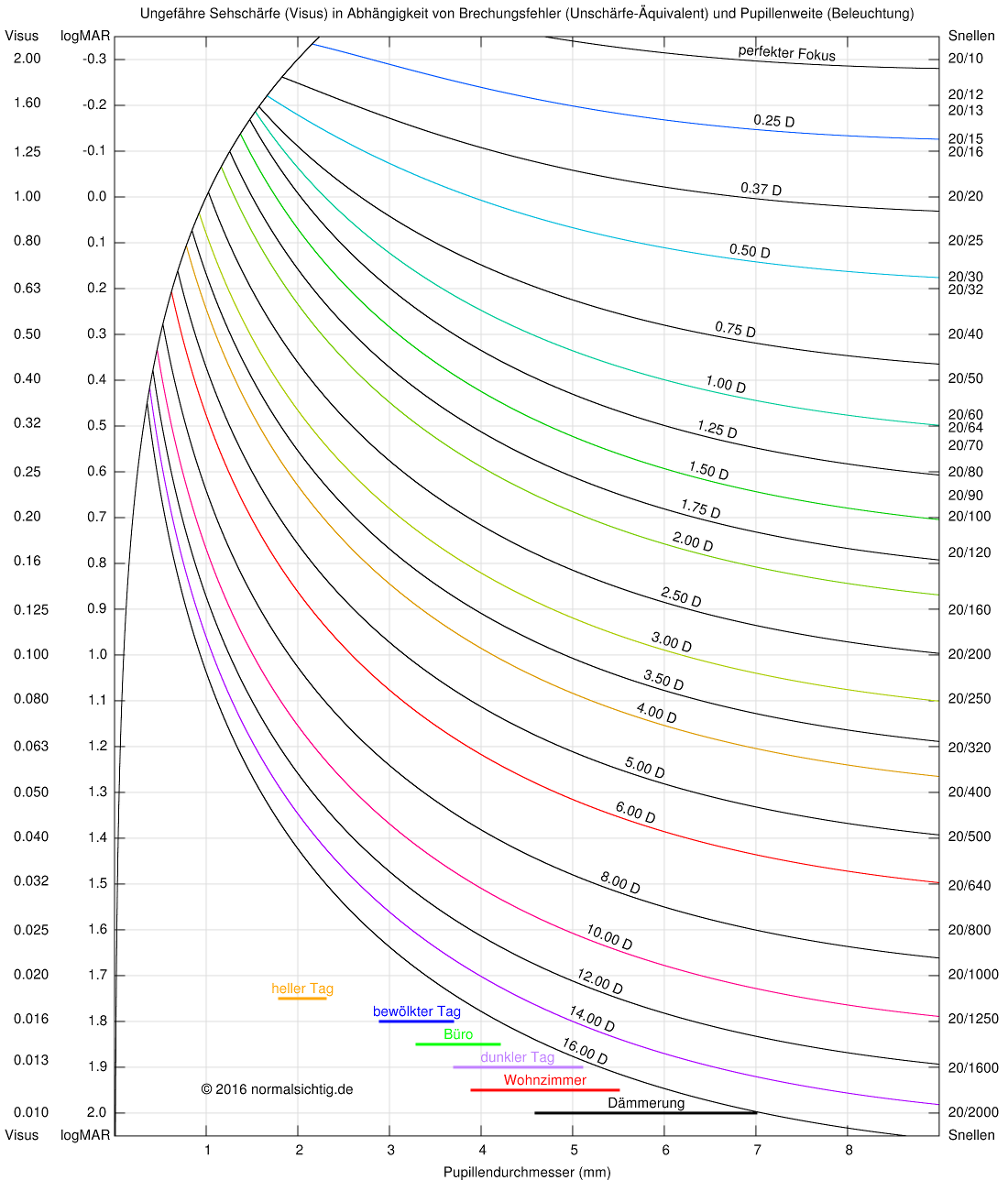
Im folgenden Diagramm ist die ungefähr zu erwartende maximale Sehschärfe bei Vorhandensein von Brechungsfehlern dargestellt. Für verschiedene Unschärfe-Äquivalente ist jeweils die Abhängigkeit der Sehschärfe vom Pupillendurchmesser (in mm) dargestellt. Dabei ist auf der y-Achse der Visus in den drei gebräuchlichen Skalen aufgetragen: ganz links der dezimale Visus, aus dem sich die Sehschärfe in Prozent durch Division durch 100 erhalten lässt, daneben (ebenfalls auf der linken Seite) die logMAR-Skala und auf der rechten Seite der im angloamerikanischen Raum verbreitete Snellen-Bruch.
Im unteren Teil des Diagramms sind zudem für einige typische Lichtverhältnisse die Bereiche des Pupillendurchmessers angegeben. Das rechte Ende einer jeden Linie (weite Pupille) entspricht dem Durchschnittswert eines 25-Jährigen, das linke dem eines 75-Jährigen und die Balkenmitte entspricht dem Durchschnittswert für eine 50 Jahre alte Person.
Bei Kurzsichtigkeit mit nicht allzu hohem Astigmatismus (Cyl höchstens halb so groß wie Sph) kann direkt der sphärische Wert (ohne das Minus) verwendet werden. Für Weitsichtigkeit, hohen Astigmatismus und zum Herauslesen von Sph und Cyl aus dem Brillenpass folgen unten die Erläuterungen.
Das Unschärfe-Äquivalent
Um einen Zusammenhang zwischen Brechungsfehler (Brillenstärke, Sehstärke) und Sehschärfe (Visus) herzustellen, wird der Brechungsfehler zweckmäßig als Unschärfe-Äquivalent (defocus equivalent) ausgedrückt. Hierzu wird zunächst das sphärische Äquivalent Seq berechnet, welches sich als Summe von sphärischer Brillenstärke Sph und der halben Zylinderstärke Cyl berechnet. Bei der Addition muss das Vorzeichen berücksichtigt werden:
Seq = Sph + ½ Cyl
Ist das sphärische Äquivalent negativ, so ergibt sich das Unschärfe-Äquivalent Ueq einfach als Summe der Beträge von sphärischem Äquivalent und der halben Zylinderstärke – diesmal beide ohne Berücksichtigung des Vorzeichens:
Ueq = |Seq| + ½ |Cyl|
Fähigkeit zur Akkommodation in der Ferne bei Weitsichtigkeit
Ist das sphärische Äquivalent dagegen positiv, muss es vor Einsetzen in die oben genannte Formel noch korrigiert werden, um Akkommodation zu berücksichtigen. Statt Seq ist dann das akkommodationsreduzierte sphärische Äquivalent zu verwenden:
Seqred = c · (Seq – t)
Dabei sind die Werte für c und t altersabhängig:
| Alter | c | t |
|---|---|---|
| 5…15 Jahre | 0,4 | 2,00 |
| 25…35 Jahre | 0,4 | 1,25 |
| 45…55 Jahre | 0,6 | 0,75 |
Ist er erhaltene Wert für das akkommodationsreduzierte sphärische Äquivalent negativ, ist stattdessen 0 zu verwenden.
Außerdem sollte noch erwähnt werden, dass die Formel bei extremer Weitsichtigkeit an dem Punkt versagt, an dem die volle Akkommodationsbreite erschöpft ist. Ab diesem Punkt zählt jede weitere Vierteldioptrie voll.
Beispiele
Ein Kurzsichtiger
| Werte aus dem Brillenpass | Berechnete Werte | ||||||
|---|---|---|---|---|---|---|---|
| Auge | Sph | Cyl | Achse | Basis | Seq | Ueq | |
| R (fern) | -1,25 | -0,50 | 165 | 0,8 | -1,25 + ½·(-0,50) = -1,50 | 1,50 + ½·0,50 = 1,75 | |
| L (fern) | -1,00 | -0,75 | 15 | 1,2 | -1,00 + ½·(-0,75) = -1,37 | 1,37 + ½·0,75 = 1,75 | |
Eine Weitsichtige (30 Jahre)
| Werte aus dem Brillenpass | Berechnete Werte | |||||||
|---|---|---|---|---|---|---|---|---|
| Auge | Sph | Cyl | Achse | Basis | Seq | Seqred | Ueq | |
| R (fern) | +3,50 | -1,50 | 155 | 1,0 | +3,50 + ½·(-1,50) = +2,75 | 0,6 · (2,75 – 1,25) = 0,90 | 0,90 + ½·1,50 = 1,65 | |
| L (fern) | +4,00 | -1,00 | 105 | 0,2 | +4,00 + ½·(-1,00) = +3,00 | 0,6 · (3,00 – 1,25) = 1,05 | 1,05 + ½·1,00 = 1,55 | |
Vektor-Addition von sphärischem Äquivalent und Zylinderstärke
Alternativ zum Unschärfe-Äquivalent wurden auch verschiedene andere Formeln vorgeschlagen, so zum Beispiel die Länge der Vektor-Summe von sphärischem Äquivalent und Zylinder, die sich wie folgt berechnet:
Veq = (Seq2 + ¼ Cyl2)½
Dabei entspricht ½ („hoch einhalb“) dem Ziehen der Quadratwurzel. Die beiden Formeln unterscheiden sich nur dann wesentlich, wenn die Zylinderstärke nicht sehr viel kleiner ist als das sphärische Äquivalent. In diesem Fall liefert die Länge des Vektors etwas bessere Vorhersagen für die Sehschärfe als das oben vorgestellte Unschärfe-Äquivalent.
Artikel (freier Zugriff): Raasch, Thomas: Spherocylindrical Refractive Errors and Visual Acuity, Optometry & Vision Science, 72:4 (April 1995), 272–275.
Abhängigkeit von den Lichtverhältnissen
Die Lichtverhältnisse nehmen auf doppelte Weise Einfluss auf die Sehschärfe:
- Der Pupillendurchmesser nimmt hauptsächlich bei Vorhandensein von Brechungsfehlern einen Einfluss auf die Sehschärfe. Dieser ist dann aber erheblich, denn je größer der Bereich, durch den das nicht richtig fokussierte Licht ins Auge trifft, desto stärker wirkt sich ein Brechungsfehler aus.
- Der Kontrast nimmt mit abnehmender Helligkeit in der Regel ebenfalls ab. Der verminderte Kontrast verringert die maximal erreichbare Sehschärfe. (Ausnahmen sind selbst leuchtende Gegenstände in der Dunkelheit, bei denen der Kontrast gegebenenfalls sogar nachts größer sein kann.)
- Der verringerte Kontrast kann dann seinerseits das korrekte Fokussieren noch einmal erschweren und somit den effektiven Brechungsfehler noch vergrößern (Nachtmyopie).
Ablese-Beispiele
Der Kurzsichtige
Für unseren Beispielkurzsichtigen mit dem Unschärfe-Äquivalent von 1,75 Dioptrien in beiden Augen lässt sich aus dem Diagramm folgendes Ablesen: unter normalen Bedingungen liegt die unkorrigierte Sehschärfe bei etwa 30%, in der Dämmerung sogar bei knapp 20%. An einem sonnigen Tag kann er es aber auch auf 70% bringen.
Die Weitsichtige
Für die Weitsichtige wäre aufgrund des ähnlichen Unschärfeäquivalents Ähnliches zu erwarten. Allerdings ist ihr linkes Auge stark sehbehindert (Basis-Visus 20%). Deshalb wäre für sie auch im grellen Sonnenlicht nicht zu erwarten, dass die Sehschärfe 20% bedeutend übersteigt. Dass aus sein rein optischen Gesichtspunkten mehr drin wäre, spielt keine Rolle, wenn die Netzhaut das scharfe Bild nicht richtig auflösen kann.
Quellen
Artikel (freier Zugriff): Jody Fay Leone; Paul Mitchell; Ian George Morgan; Annette Kifley; Kathryn Ailsa Rose: Use of Visual Acuity to Screen for Significant Refractive Errors in Adolescents – Is It Reliable?, Archives of Ophthalmology, 128:7 (Juli 2010), 894–899.
Artikel (kein freier Zugriff): Jack T. Holladay; Michael J. Lynn; George O. Waring III; Mary Gemmill; Gordon C. Keehn; Brooke Fielding: The Relationship of Visual Acuity, Refractive Error, and Pupil Size After Radial Keratotomy, Archives of Ophthalmology 109:1 (Januar 1991), 70–76.
Artikel (freier Zugriff): B Winn; D. Whitaker; D B Elliott; N J Phillips: Factors affecting light-adapted pupil size in normal human subjects, Investigative Ophthalmology & Visual Science, 35:3 (März 1994), 1132–1137.
Artikel (kein freier Zugriff): Thorn, Frank; Schwartz, Faye: Effects of Dioptric Blur on Snellen and Grating Acuity, Optometry & Vision Science, 67:1 (Januar 1990), 3–7.